In the expansive tapestry of world history, certain civilizations stand out for their remarkable contributions to the development of mathematics. Mathematics, often regarded as the universal language, where it has played a pivotal role in shaping civilizations across the globe. While the contributions of ancient Greek, Roman, and Chinese mathematicians are well-documented, the mathematical achievements of the Maya civilization in Mesoamerica are often overlooked. However, delving into Maya mathematics reveals a sophisticated numerical system and advanced concepts that greatly influenced various aspects of ancient Maya society. This article endeavors to shed light on the profound influence of Maya mathematics on the societal, architectural, and cultural landscape of ancient Mesoamerica, offering a comprehensive exploration of a lesser-known chapter in the history of mathematics.
The Mayan mathematical understanding
Before we go through Maya mathematics, we may introduce the Maya people. The Maya was an ancient Mesoamerican civilization that flourished in the tropical lowlands of present-day Mexico, northern Belize, Guatemala, Honduras, and El Salvador. They spoke around 30 languages, with over five million speakers mostly bilingual in Spanish. Before the Spanish conquest, the Maya civilization was renowned for its complex and advanced achievements in various fields, including architecture, mathematics, astronomy, art, and hieroglyphic writing.
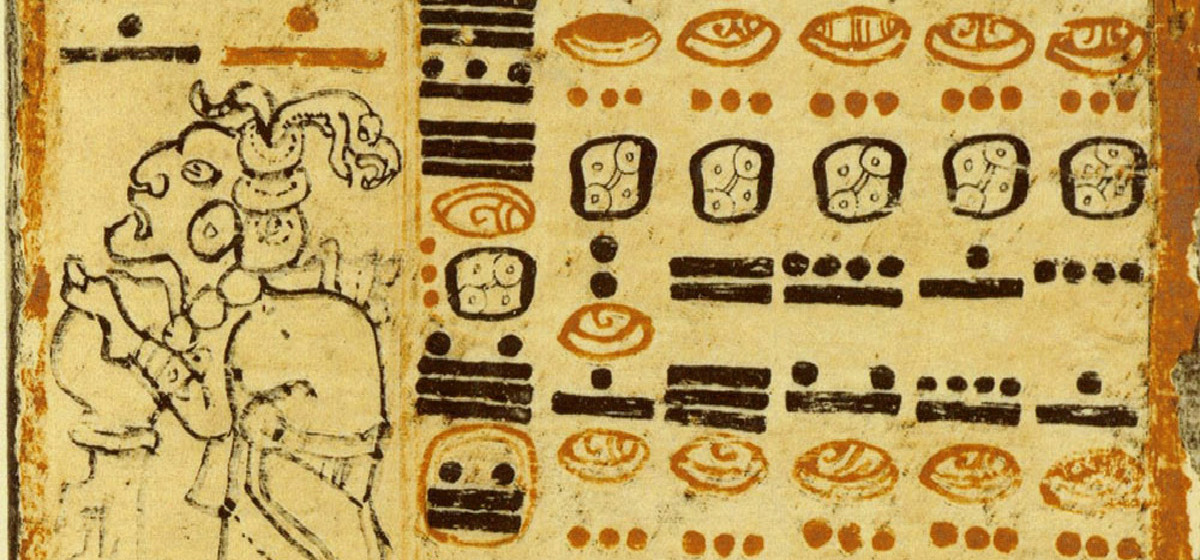
On the website Planet Archaeology, under the topic Maya Number System by Dr. Patrice Bonnafoux, readers can explore the ancient Maya civilization’s number system. Dr. Bonnafoux provides a detailed explanation of this sophisticated system, offering insights into how the Maya understood and utilized numbers. This resource allows for an in-depth appreciation of the intricacies of Maya numerals and their cultural significance. At the heart of Maya mathematics lies a numerical system of remarkable complexity and elegance. Unlike the base-10 system commonly employed today, the Maya utilized a vigesimal (base-20) system, demonstrating a nuanced understanding of numerical representation. Central to this system were symbols representing units, fives, and zeros, intricately combined to express numbers of varying magnitudes. Through a sophisticated combination of positional notation and mathematical principles, the Maya devised a highly efficient counting system capable of addressing the demands of their complex society.
On the website Special Report (FT), they use Maya mathematics in classrooms in Mexico, where we can see the revolution of Maya mathematics. In a classroom in Celtún, a village nestled in the state of Yucatán, Mexico, eight-year-old Verónica Yuritzi Martín Puc engages in a unique approach to learning mathematics. Instead of traditional methods, she utilizes a system invented by her Maya ancestors thousands of years ago. With a simple grid drawn on her desk, Yuri places dried black beans and shells of dried pasta to represent numbers, following the ancient Maya counting system.
Yuri’s teachers, recognizing the challenges of the modern education system in teaching basic numeracy and literacy, have embraced this ancient method to breathe new life into mathematics education. This approach draws inspiration from the sophisticated mathematical and astronomical knowledge of the Maya civilization, which flourished across southern Mexico and Central America from around 2000 BC to AD 900.
Celtún, situated near the awe-inspiring ruins of Chichén Itzá, serves as a poignant reminder of the Mayan legacy. By revitalizing the ancient counting system, Yuri and her peers connect with their cultural heritage while mastering fundamental mathematical concepts in a way that resonates deeply with their community’s history and identity.
The Mayan mathematical system is simple: a bean equals one unit, five beans make a bar, and zero is a pasta shell. Numbers are arranged vertically from top to bottom, with the bottom row representing units (0-9), the next row tens, then hundreds, and so on. Teacher Mary Carmen Che Chi demonstrates this by having children roll a dice and move beans on grids to match the numbers, thereby enhancing their understanding and enjoyment of math.
The Ignacio Ramírez Calzada primary school introduced the Maya number system to improve basic math skills under the new headmaster José Manuel Cen Kauil. Using low-cost materials like cardboard grids and corn kernels, this method connects students with their cultural heritage while developing logical reasoning. The initiative traces back to physicist Luis Fernando Magaña’s discovery of the Maya counting system in 1979, leading to its adaptation for teaching.
In 2009, Magaña began teaching Maya math in Yucatán’s indigenous schools, successfully incorporating it into the curriculum to help children master fundamental arithmetic. The method has shown promise for broader implementation across Mexico, with national curriculum guidelines now emphasizing mathematical reasoning and positive attitudes towards math. Indigenous schools have seen significant improvements since introducing Maya math: Students achieving “excellent” grades increased from 0.1% in 2006 to 8.3% by 2011, while those ranked “insufficient” decreased from nearly half to 29.4%. Teachers report that Maya math enhances decision-making, confidence, and understanding. Prof. Magaña believes that it can bridge social divisions and boost self-confidence, helping to combat educational inequality in Mexico.
The Mayan zero concept
The mathematical sophistication of the Maya civilization is a subject of considerable academic interest. Zero is one of the most important numbers in mathematics; without it, we cannot do accurate counting and advanced calculations would be impossible. While we have seen how Maya mathematics can be applied in modern education in Mexico, this part of the article aims to explore the profound influence of the number zero on our daily lives and its use in ancient Maya civilization.
The Mayans developed a highly sophisticated calendar system, which included intricate astronomical calculations and the revolutionary concept of zero. This system allowed them to achieve remarkable precision in timekeeping and forecasting astronomical events.
The prediction that the world would end in 2012, often attributed to the Maya calendar, sparked significant interest and speculation. This prediction stems from a misinterpretation of the Maya Long Count calendar, which completed a major cycle on December 21st, 2012. Contrary to popular belief, the end of this cycle did not signify an apocalyptic event but rather the conclusion of a significant period in the Maya calendar system.
The concept of zero was crucial for Mayan mathematics as it allowed for complex calculations, accurate data recording, and the development of an advanced calendar system. This innovation revolutionized their numerical notation, making arithmetic operations significantly more efficient and enabling scientific advancements in various fields. The Maya’s sophisticated understanding of zero not only underscores their intellectual achievements but also highlights their contribution to the global history of mathematics.
In the article “The Maya Calendar: why 13, 20 and 260?”, Polyakova writes about how the ancient Mayan utilized the head of Draco as a critical astronomical and mathematical unit in their calendrical system. This constellation’s head was considered a measure of time and the starting point in the Tzolkin calendar, depicted as a dragon’s head. For the Maya, mythological interpretations of celestial patterns were a way to understand reality. Their sophisticated calendar system, beginning on August 13, 3114 BCE, according to the GMT correlation, combined three systems: the Long Count, Haab, and Tzolk’in.
The Long Count tracked extensive periods using units like Kin (day), Winal (20 days), Tun (360 days), Katun (7,200 days), and Baktun (144,000 days). The Haab, a 365-day solar calendar, tracked seasons, while the Tzolk’in, a 260-day cycle, was used for religious events and divination. Together, these formed the Calendar Round, repeating every 52 Haab years or 73 Tzolkin cycles, equaling 18,980 days.
The Tzolk’in connection to Draco’s head, a stable point in the northern sky, reflects a tradition of using astronomical observations for timekeeping. The pole of the ecliptic, near Draco, served as a constant reference. Ancient civilizations across Eurasia and North America, including the ancestors of Native Americans, used similar celestial markers.
The Maya’s addition of the 260-day Tzolk’in to their calendrical system distinguished their timekeeping, including epochs lasting 5,125 years each. The end of the fifth epoch on December 21, 2012, marked a renewal rather than an apocalyptic event, fitting into the Maya’s cyclical view of time. Their calendar’s vast timespan, totaling 41,341,050,000,000,000,000,000,000,000 years, arose from their avoidance of fractional numbers, favoring large integers and the number 20. The Maya’s integration of astronomical observations with mathematical cycles thus created a precise and enduring calendrical system.
Comparing the modern Gregorian calendar with the ancient Maya calendar
The Gregorian calendar was introduced by Pope Gregory XIII in 1582, and is the calendar system most widely used today. It is a solar calendar based on a 365-day year, divided into 12 months. To align the calendar year with the astronomical year, a leap year is added every four years, except for years that are divisible by 100 but not by 400.
The Maya calendar system is more complex, incorporating several interlocking cycles, the most notable of which are the Tzolk’in, the Haab’, and the Long Count, as described above.
In mathematical principles we see that in the Gregorian calendar, the concept of zero is used indirectly within the AD/BC system which is commonly used in the Western world for dating historical events – although there is no year zero, as the calendar transitions directly from BC (Before Christ) to AD (Anno Domini). Conversely, the Maya calendar employs an explicit symbol for zero, depicted as a shell-like glyph, which is crucial for their vigesimal (base-20) number system. This explicit use of zero allows for precise calculations and record-keeping in the Maya calendrical and numerical systems.
The Gregorian and Maya calendars reflect different cultural approaches to timekeeping, influenced by their respective societies’ needs and astronomical observations. The Gregorian calendar emphasizes solar years and the Earth’s orbit, while the Maya calendar incorporates multiple cycles for religious, agricultural, and historical purposes. Both systems, however, demonstrate sophisticated mathematical understanding and the pivotal role of zero in their construction.
Butsabakorn Lamthaisong is a M.Sc. student in Mathematics, University of Southern Denmark